 Click
for Site Directory
Click
for Site DirectoryTheory of Barrage Balloons
These balloons were not simply gas bags full of lighter than air hydrogen, they were developed using a range of experimentation techniques and
practical experience following on from the use of balloons in WWI. Between the wars much research took place into refining the concept and
ensuring the design and function was optimum for the role the balloon had to play. The Air Ministry had a number of sites that were used to test
different designs and ideas on balloons, including wind tunnel tests.
The principle of flight for these balloons was simple enough, the uplift of the hydrogen gas was such that it gave more uplift to the balloon than
the balloon weighed. In other words if you remember the Law of Archimedes that states;" A body be completely immersed in a fluid it displaces a
quantity of fluid equal to its own volume." - This applies equally to ships, submarines and airships and balloons.
If the displacement of fluid or air has a weight less than the body immersed in it, it will sink to the bottom, if the displacement is a weight greater
it will float to the surface. If you consider a balloon floating in the air as having a degree of support that gives it an up thrust you can see how
similar the situation is for say a wooden object placed in water.
The up thrust is dependent on the type of gas used, the volume of the gas and the altitude to be attained.
The "Lifting Power" of a balloon can be calculated for various gases under identical conditions.
All we need to do is calculate the weight of air that the balloon will displace at a specific altitude and then subtract from that figure the total
weight of the balloon in question.
If a balloon was of 80,000 cubic feet capacity and was to fly at 19,000 feet where the atmospheric pressure in inches of mercury is 15 inches as
opposed to 30 inches at sea level, this means that the air pressure at that height is half that of sea level .So the atmosphere at 19,00 feet weighs
15/30 x 75 lbs per 1000 cubic feet, or 37.5 lbs per 1000 cubic feet.
If we used coal gas the calculation would run like this:
Weight of atmosphere 80 x 37.5 = 3000 lbs
Weight of Balloon = 1200 lbs
Gross Displacement lift = 1800 lbs
Weight of 80,000 cubic feet of coal gas at 18.75 lbs per 1000 cubic feet = 1500 lbs
NET LIFT WITH COAL GAS = +300 lbs
Add weight of pilot 150 lbs = -150 lbs
SURPLUS LIFT AT 19,000 feet ALTITUDE = +150 lbs
This means the balloon will rise to this altitude with a lift of 150 lbs.
If we used HYDROGEN gas the calculation would run like this:
Weight of atmosphere 80 x 37.5 = 3000 lbs
Weight of Balloon = 1200 lbs
Gross Displacement lift = 1800 lbs
Weight of 80,000 cubic feet of coal gas at 18.75 lbs per 1000 cubic feet = 200 lbs
NET LIFT WITH COAL GAS = +1600 lbs
Add weight of pilot 150 lbs = -150 lbs
SURPLUS LIFT AT 19,000 feet ALTITUDE = +1450 lbs
This means the balloon will rise to this altitude with a lift of 1450 lbs.
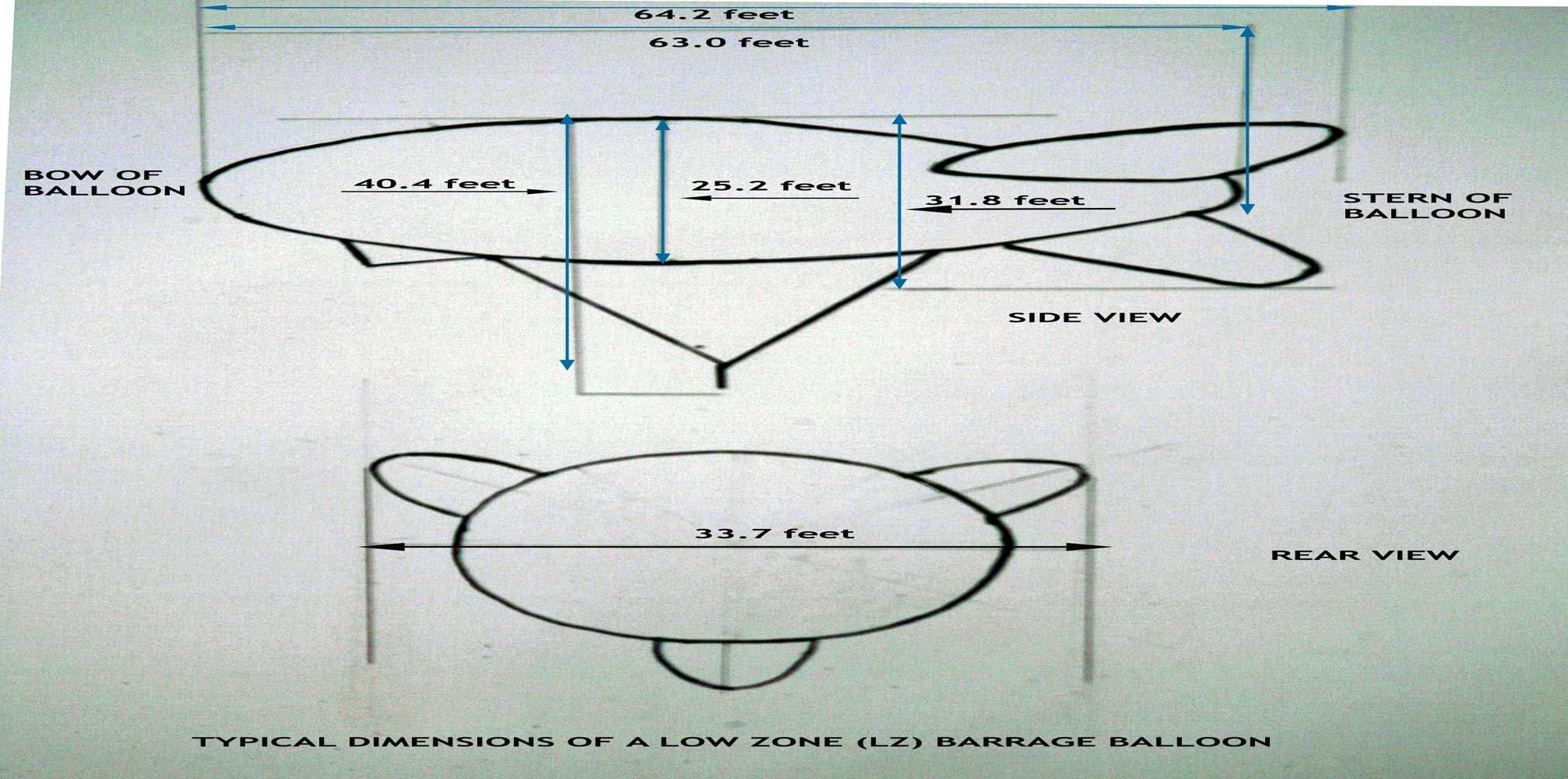
Dimensions of Barrage Balloons
The principle dimensions were:
Overall Length (with stabilisers inflated) : 64.20 feet or 19.50 metres
Length of Gas Envelope : 63.00 feet or 19.15 metres
Maximum Diameter : 25.20 feet or 7.70 metres
Width Overall (with stabilisers inflated) : 33.70 feet or 10.30 metres
Height Overall to bottom of rudder : 31.80 feet or 9.70 metres
Height of Balloon Rigging to Point of Attachment : 40.40 feet or 12.30 metres
Gas Volume : 19,150 feet or 54.20 metres
Weight of Balloon : 565 pounds or 256 Kilos
In flight the angle of pitch would vary depending on the gas purity and the wind speed. In still air a 3 degree pitch with bow up was maintained. If
the wind was at 60 m.p.h. then a pitch of 11 degrees bow up was maintained. Both these examples are allowing for maximum purity. The bow will
always fly higher than the tail with maximum purity.
Cable Tensions vary with the wind speed & gas purity. In a steady wind speed of 60 m.p.h. gas purity of 88% the cable tension was 2,540 lbs, If the
gas purity rose to 98% then the tension in the cable was 2,970 lbs. The average tensions were around 780 - 1120 lbs, if it exceeded the 1790 lbs
then the situation was dangerous and the cables would break.
The barrage balloon is divided into two envelopes. The upper envelope was filled with hydrogen gas and the lower air envelope or ballonette was
filled with air. The role of the ballonette was to compensate for the loss of gas as the balloon ascended and served to preserve the streamline
form of the balloon.
When the balloon is inflated it is manned and handled up to 20 metres to keep its nose into the wind. This permits the stabilisers, which have air
scoops, to take up air and become inflated.
As the balloon ascends (the order was "let up!") and the air becomes less dense the atmospheric pressure reduces, this in turn allows the gas in the
balloon to expand. This expansion forces a pressure down onto the ballonette. This pressure causes the internal valve lines to be pulled down and
at a pre-determined pressure forces the exhaust valve to open allowing hydrogen gas to escape until normal pressure is reached. At this stage the
exhaust valve will automatically close.
When the balloon was brought down (the order was "haul down!") to a lower altitude the gas would contract due to a raise in the atmospheric
pressure. This would cause the balloon to lose shape: it was at this point that the ballonette would take on its function. The air blowing against
the air scoop is able to force its way through into the ballonette due to the shrinkage of the gas envelope and fill out the slack of the upper gas
envelope.
The L.Z.or Low Zone balloon was designed by the Air Ministry in 1934 and was intended for low barrage work only. The low zone altitude went up
to about 5,000 feet and this height could be exceeded by a further 900 feet if the hydrogen in use was very pure ( of the order of 98%).
The purity of hydrogen was measured on site by use of a little known apparatus invented by Schiling.
THE SCHILING GAS PURITY METER
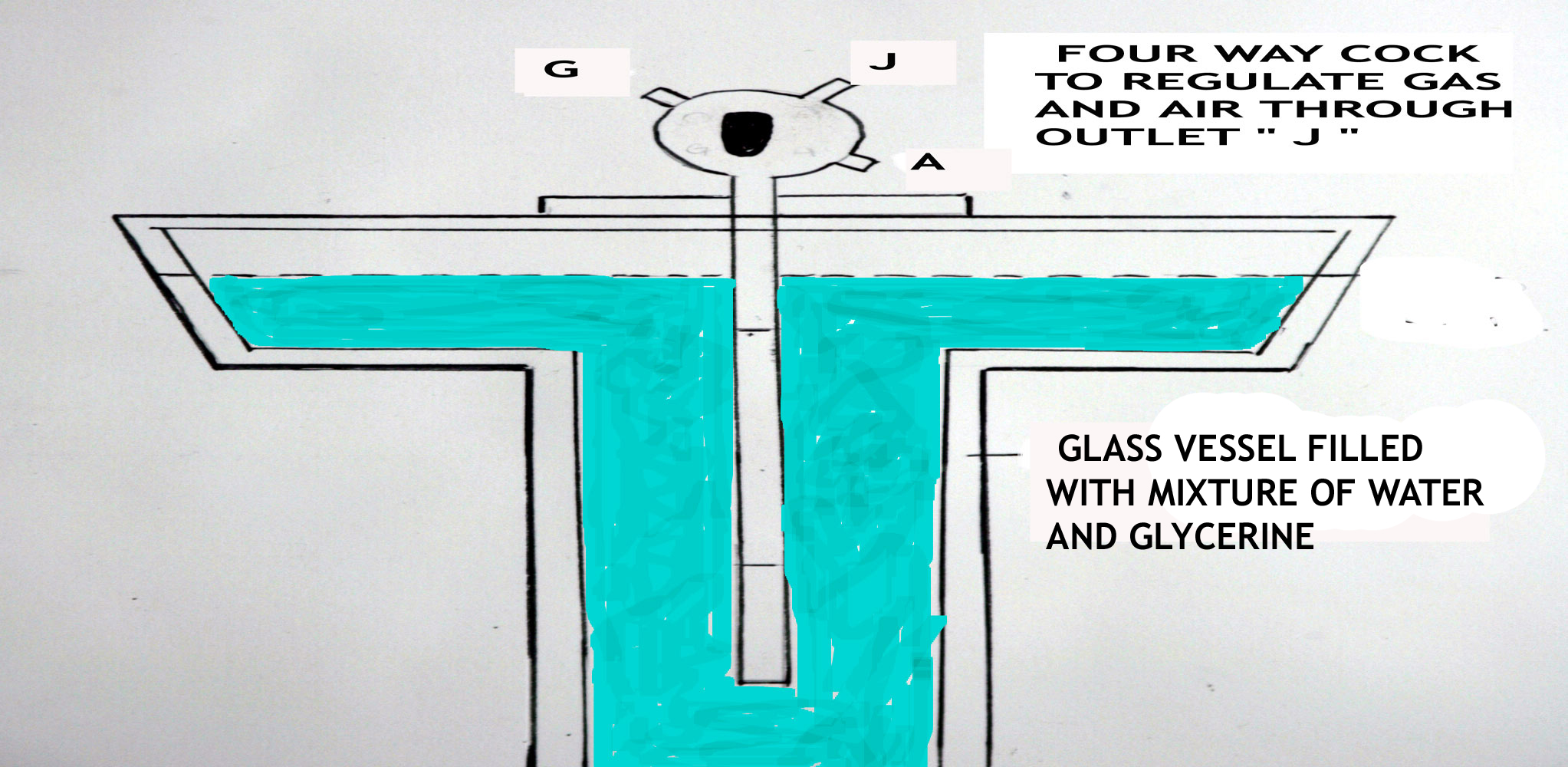
The equipment had to be basic, and simple to operate and give consistent readings.
This consisted of a four-way cock system in glass.
The idea was that the system was lifted up with the cock open to the atmosphere. It was then raised until the end of the tube was level with the
water/glycerine mixture in the apparatus but was not exposed. The tube was placed back on its seating and the cock now turned to junction (J). A
stop watch was started to measure the time it took for the water/glycerine mixture level to rise between two markings on the glass tube. This
was repeated for 3 measurements and then the average time was noted. The water/glycerine mixture rose as the air or gas was forced out through
a small uniform aperture at J. Depending on the gas density this would take less time for a pure gas and longer for a non-pure gas.
The exercise was now repeated but this time having turned the gas cock to G for hydrogen gas. It was necessary to purge the glass tube for 3
measurements and then measure the time for the water/glycerine mixture to rise between the two marks using the hydrogen gas.
The operator would now have a time measurement for the air and one for the hydrogen gas. Remember all this was done without lighting any
cigarettes or pipes due to the highly explosive nature of hydrogen!!
The purity was calculated using a formula:
% Purity (P) = 1- (Time Hydrogen/ Time Air)2 / 0.0093
For example: If the Air time was 40 seconds and the Hydrogen time was 19 seconds, the purity was:
% Purity = 1 -(19/40)2 / 0.0093 = 1- 0.2256 / 0.0093
% Purity = 0.7744/ 0.0093 = 83.25%
If the purity fell below 86% then the balloon had to be deflated and refilled
The more pure the hydrogen the higher it would fly as shown by these calculations typical of the day.
Height of Balloon = H, Weight of Balloon = W,
Weight of cable per 1000 foot (e.g. a KBS was 100lbs per 1000 foot), = w,
Lift of Balloon= (88% purity =1223 lbs) (13.9 lbs per 1% purity).
So if using 88% pure hydrogen: The height could be calculated using the following formula.
Height = W + wH = ( L-LH ) x 1/30
Height = 565+100H =1223-(1223H x 1/30)
565 + 100H= 1223-41H
100H + 41H = 1223-565
141H = 658
H= 658/141 = 4.60
Thus height would equal 4,600 feet.
If the gas was 94% pure then:
1%=1223 x 1/88 and 94%=(1223 x 94) x 1/88 = 1306 lbs of lift or 94 x 13,9 = 1306 lbs
One of the peculiarities of Barrage Balloons was loss of gas, this was due to the fabric manufacture and was sometimes due to holes in the
material. However the gas molecule was very small compared to the molecules of rubber and with the gas being pressurised and subjected to
temperature variations then there was always a degree of gas permeability through the balloon fabric. The Air Ministry appears to have been
somewhat naive in the early days of the war, believing that once the balloon was filled with hydrogen and sent aloft it would not lose any gas at
all. This was soon shown to be wrong and balloons ended up being topped up onan almost daily basis.
Over time a rough rule was established:
1.If the balloon lost volume but the gas purity was unchanged then it was highly likely that the hole was in the upper part of the balloon.
2.If the balloon gas volume was the same but the gas purity was reducing then it was highly likely that the hole was in the lower part of the balloon.
In general these two rules proved to be correct.